|
تفریح با ریاضی بانک سوالات-معما-هوش-
| ||
|
لینک دوستان
|
نمایش هندسی اعداد بر روی محور اعداد (خط حقیقی) همیشه از اهمیّت خاصی برخوردار بوده است. البته نمایش اعداد طبیعی،اعداد صحیح و اعداد گویا نسبتا ساده است ولی نمایش هندسی اعداد گنگ (اصمّ) نیازمند اطلاعات هندسی بیشتری می باشند حتی بعضی از مواقع مساله بغرنج تر می شود به این معنی که همه اعداد گنگ ترسیم پذیر نیستند.البته ما بنا نداریم به صورت پیشرفته وارد این بحث شویم بلکه فقط می خواهیم در حد ریاضیات اول دبیرستان مطالبی را ارائه دهیم. به زعم تاریخ به نظر می رسد اولین عدد گنگ که بشر به آن دست یافته است
در حد کتاب درسی معمولا اعداد گنگ برای ساختن طول هایی به اندازه اعداد گنگ بالا از قضیه فیثاعورس کمک می گیریم.روش ساخت راذیلا شرح می دهم: برای ساخت طولی به اندازه برای ساخت طولی به اندازه برای ساخت طولی به اندازه برای ساخت طولی به اندازه 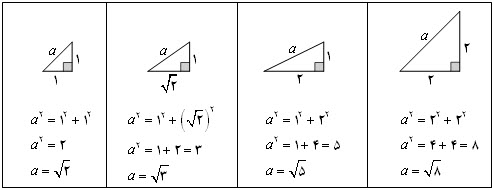 برای پیداکردن نقطه متناظر با اعداد گنگ کافیست ما همین مثلث ها را روی محور اعداد بسازیم.مثلا برای پیدا کردن نقطه متناظر با عدد
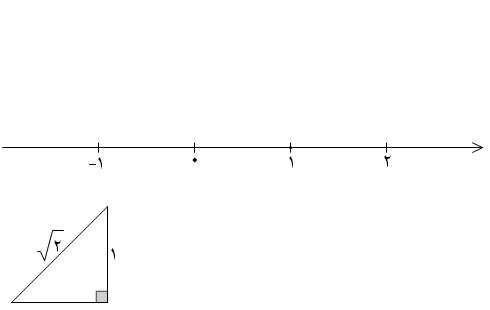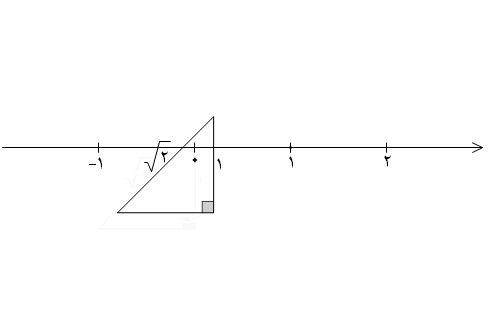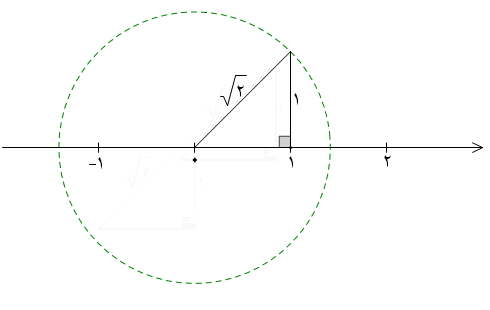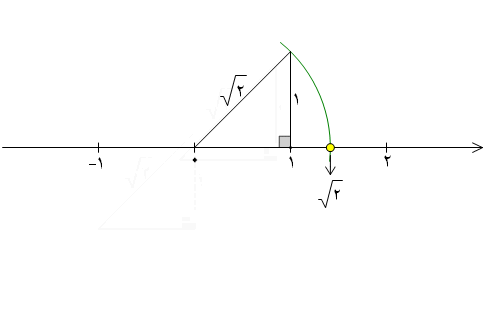 در ادامه نقاط متناظر با اعداد گنگ دیگری را روی محور نمایش می دهیم.
رسم 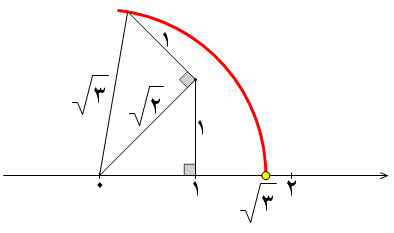 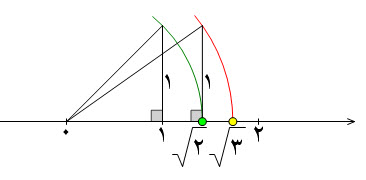 بقیه بحث را در ادامه مطلب ببینید... 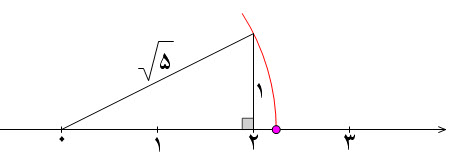 روش رسم
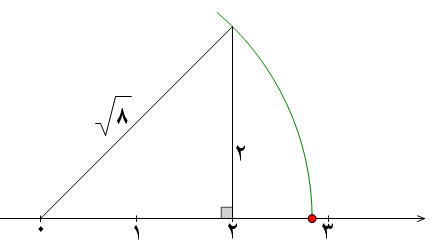 در ادامه اعداد گنگی را رسم می کنیم که به صورت ترکیب یک عدد صحیح و یک عدد رادیکالی می باشند:
 
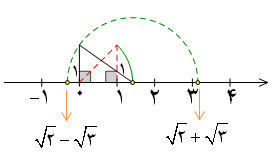
برچسب‌ها: |
|
| [ طراحی : پرشین اسکین ] [ Weblog Themes By : Persian Skin ] | ||
تبادل
لینک هوشمند